Olympic history

Participating athletes and medal count in the Modern Olympic Games over 120 years. Analysis of athletes and national teams from 1896 until 2016 and the influence of population and GDP per capita on the medal count of the nations in 2016.

Updates and Note

Updated 2022-08-05: Ported blog to quarto. Post could be rendered, but minor issues might have been introduced.

Updated 2021-07-29: The Olypmic dataset was presented as #TidyTuesday data in week 31 of 2021. I revised the last plot of this post as my contribution for #TidyTuesday.
Updated 2021-02-13: Added bar chart race.

Introduction

This is a non-systematic analysis of historical data on the Modern Olympic Games. The first Olympiad of the Modern Era organized by the IOC¹ were held at Athens in 1896. Inclined readers might want to read the extensive Wikipedia article.

For the summary and the conclusions you can skip the analysis and jump to Conclusions and Summary.

Important note: I’m not a real follower of the Olympic Games in general, nor did I follow up with any of the disciplines and athletes in particular before. If any of my “findings” are well known facts in the world of the Olympic Games, please excuse my ignorance and enjoy, that this fact is also represented in the underlying data.

Idea and Materials

The Idea

A question came to my mind when finding the Olympic Games dataset on kaggle: “Can money buy medals?”²

Other questions I had from the beginning were:

• How did the disciplines change over time?
• What are the top scoring nations?
• What factors improve the odds to win a medal: for this, population figures and economic data from gapminder will be called in.

As you’ll see, more interesting findings will be found on the way.

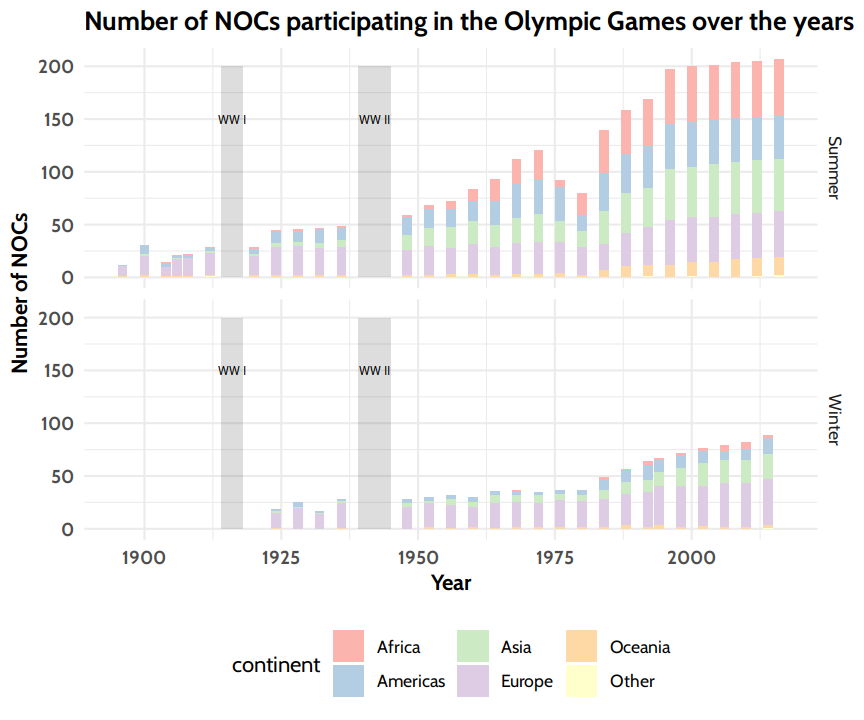
At the time of writing there are 206 NOCs³ regularly sending athletes to the competitions. The number grew over time, so not all current NOCs are included in the analysis. This development is one of the aspects I’ll focus on.

Historical Olympic Data

The dataset comprises biographical data on the participating athletes (age, gender, body measurements, …), the disciplines and specific events they attended as well as the medals they won. This is one of the more popular datasets on kaggle, and many have worked on this before me. I hope to bring some new aspects in, by combining the data with the gapminder dataset.

Acknowledgements

The data was hosted on kaggle by rgriffin under a CC0: Public domain license. The data was scraped from http://www.sports-reference.com/. The scripts rgriffin developed to scrape and rectangle the data can be found in this github repo. The credits and thanks for composing the data go to rgriffin and to the people at www.sports-reference.com for collecting them in the first place.

The Rio 2016 logo used in the last plots was downloaded from https://commons.wikimedia.org/wiki/File:Rio_2016_logo.svg Credits: National Olympic Committee, Public domain, via Wikimedia Commons

Population and Economic Data

To analyze the influence of population size and economic markers on the “outcome” of the Olympic contenders I used data from the gapminder foundation. They use data e.g. from the World Bank “to fight devastating ignorance with a fact-based worldview everyone can understand”⁴. They achieve this e.g. by giving talks and offering teaching materials. They also provide the public with the underlying data.

Attribution

The above mentioned data is FREE DATA FROM WORLD BANK VIA GAPMINDER.ORG, released under the CC-BY LICENSE

Athletes and NOCs over time

First, let’s load the required packages, read the data, enrich the NOC data with the corresponding continent…

…and then inspect the data.

Inspecting the Historic Data

Story line

There are 271116 rows and 15 variables in this dataset. The table below only shows the first 100 rows. As you can see, there are many NA’s, especially in the body measurement columns, as this was not systematically recorded in the early Olympic Games. As I’m not focussing on these columns, I can ignore this for the moment.

The number of sports included to the games varied over time. Since the 1980s the number grew with each year until the year 2000. During the last five events (2000, 2004, 2008, 2012 and 2016) the number was almost stable at 34 during summer events and 15 during winter events. WW I / II: Breaks due to World Wars I and II.

The number of NOCs that participated in the Olympic Games over time. WW I / II: Breaks due to World Wars I and II.

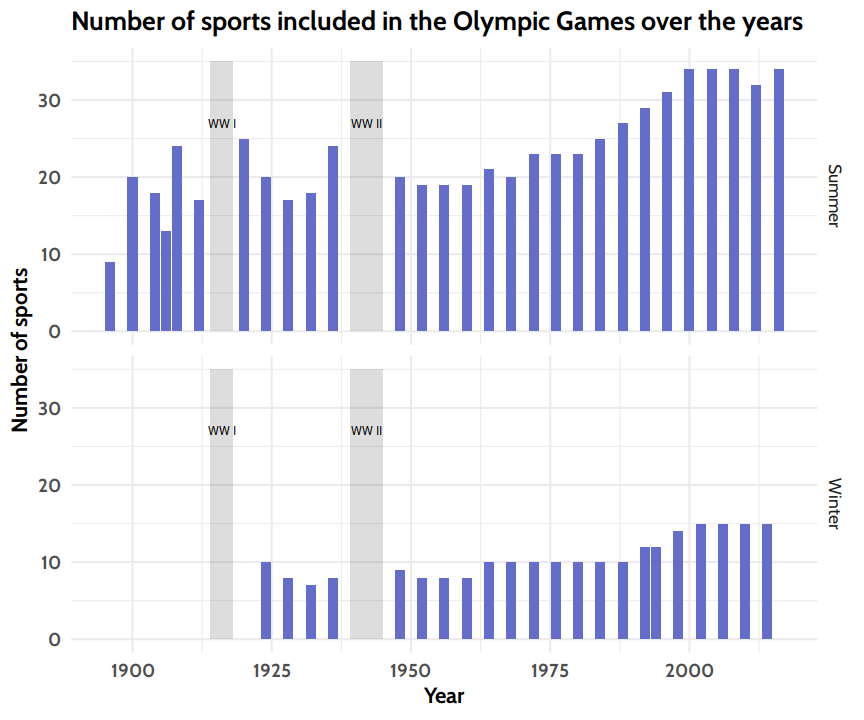
Below deck

It is always good practice to read the manual or other explanatory material provided by the author of the dataset especially to know what the variables represent. In addition I like to comprehend a few critical components myself to facilitate the later analysis. In this case I wanted to understand the way, the medals for each competition are implemented in the dataset.

Events and Medals

From inspecting the data we can see, that each row corresponds to an athlete participating in a single event, where ‘event’ means a particular match or competition where medals are awarded in the end. So e.g. the Sport “Judo” comprises separate weight classes each for female and male athletes and there are bronze, silver and gold medals within each event. For men’s Judo the Events in 2016 were: Judo Men’s Half-Middleweight, Judo Men’s Extra-Lightweight, Judo Men’s Heavyweight, Judo Men’s Half-Lightweight, Judo Men’s Lightweight, Judo Men’s Half-Heavyweight, Judo Men’s Middleweight.

If no medal was won, the ‘Medal’ column is NA, otherwise the value is either “Bronze”, “Silver” or “Gold”.

As a quick test, let’s see if there are any duplicates or wrong medal attributions in the men’s judo sport in 2016.

This was rather unexpected for a single competitor discipline: in all events two bronze medals were awarded. A quick research revealed, that this is not an error in the data collection, but rather a feature of the Judo Competitions due to the selection process during the final rounds.⁵

We should definitely keep this in mind, in case we touch this sport in a later step!

To check if there is a similar “problem” in any other sport, I repeated the above analysis regardless of the event and year:

There are quite many events with n > 1 medals, but all seem to be team competitions, in which it is plausible to have several gold, silver and bronze medals. For now this is sufficiently clarified for me.

Number of Sports in more detail

I wanted to investigate the “dent” in the number of sports in the summer 2012 Olympiad. I therefore compared the sports included in the last five summer Olympiads and found that there are 32 “constant” disciplines, while Baseball, Golf, Rugby and Softball were not in all five Olympiads.

#> # A tibble: 4 × 2
#>   Sport        Appearances_within_last_five_Olympiads
#>   <chr>                                         <int>
#> 1 Baseball                                          3
#> 2 Golf                                              1
#> 3 Rugby Sevens                                      1
#> 4 Softball                                          3

How were these sports distributed over those last five summer Olympiads?

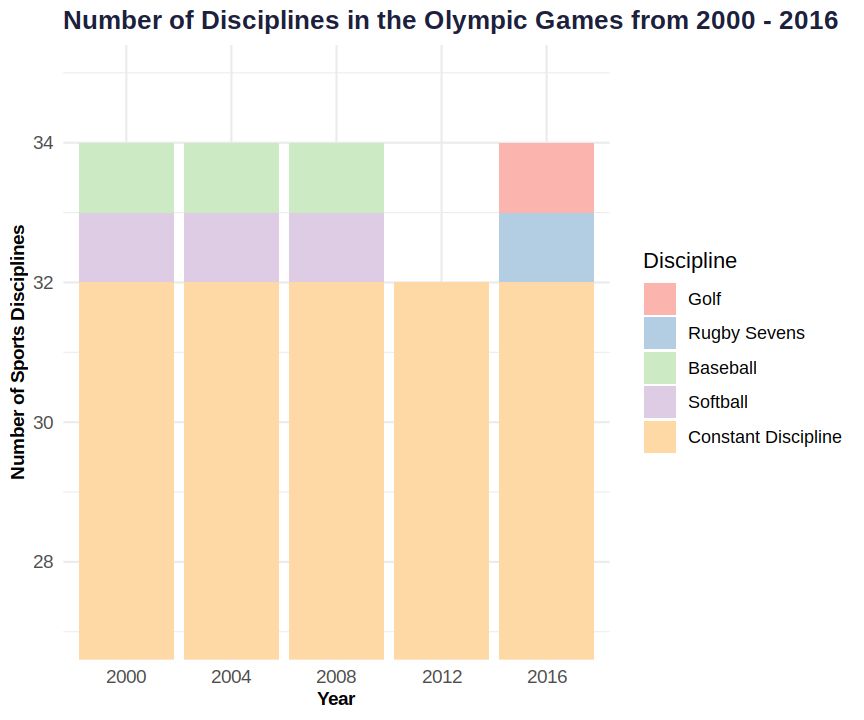
Apparently Base-/ Softball were discontinued after 2008 and they were replaced only in 2016 by Golf and Rugby Sevens, resulting in the “only” 32 disciplines in 2012.

That’s it for this “below deck” section. Let’s get back to the main story right below!

If you want to see more than just the main story line of this post, and read results that didn’t make it to the main part, you can check out the “Below deck” sections. There I might also document intermediate steps that are necessary to perform but not contributing to the story.

Top Scoring Athletes

In this section I’d like to answer three questions:

• How many Olympic Games did each athlete attend?
• Who appeared most often and in what discipline?
• Who won the most medals during Summer and Winter Games?

How many Olympic Games did the athletes attend?

We need an overview on the scales we’re talking about here: is three Summer Games a lot? Is 5 Games common?

To determine the distribution of the number of Games, single athletes have attended over the course of their career, I plotted them on a bar plot. As it turns out, the curve is exponential⁶, and there are athletes who attended more than seven Games both for female (F) and male (M) athletes:

The distribution of athletes over the number of Olympic Games they attended. For both male (M) and female (F) athletes the distribution is approximately a falling exponential curve. For better visibility the y-Axis is on a logatithmic scale.

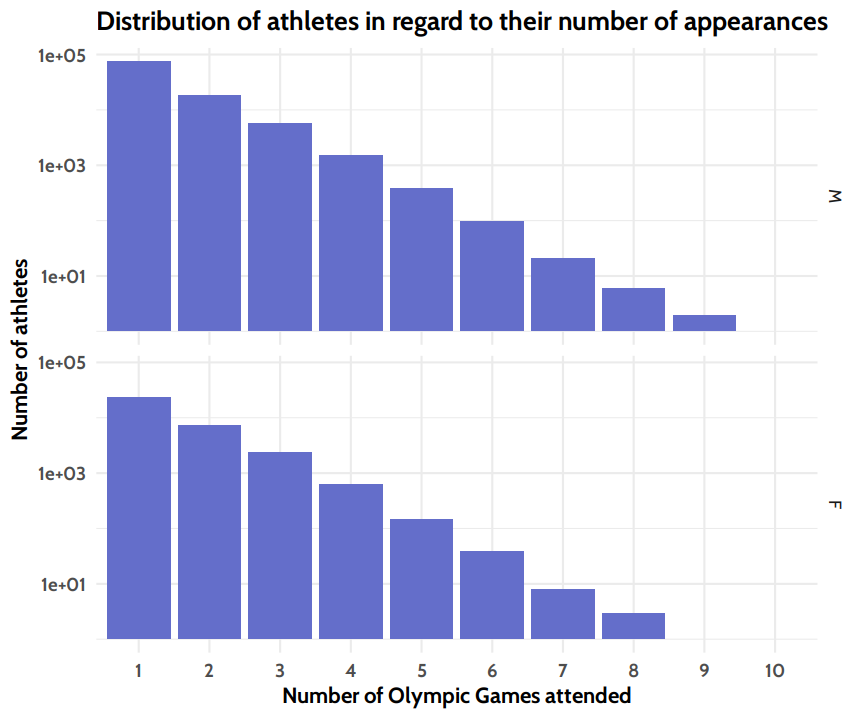
So how many do only appear on one Season?

#> # A tibble: 1 × 1
#>   one_timer_frac
#>            <dbl>
#> 1          0.726

This means, that more than 70% of all athletes only appear once on an Olympic Game.

Who appeared most often and in what discipline?

Top scoring female athletes:

#> # A tibble: 10 × 3
#>    Name                                               Olympic_Games Sport       
#>    <chr>                                                      <int> <chr>       
#>  1 "Nino Salukvadze (-Machavariani)"                              8 Shooting    
#>  2 "Lesley Allison Thompson-Willie"                               8 Rowing      
#>  3 "Josefa Idem-Guerrini"                                         8 Canoeing    
#>  4 "Jasna ekari (Brajkovi-)"                                      7 Shooting    
#>  5 "Theodora Elisabeth Gerarda \"Anky\" van Grunsven"             7 Equestriani…
#>  6 "Tinne Eva Caroline Wilhelmsson-Silfvn"                        7 Equestriani…
#>  7 "Oksana Aleksandrovna Chusovitina"                             7 Gymnastics  
#>  8 "Yekaterina Anatolyevna Khodotovich-Karsten"                   7 Rowing      
#>  9 "Jeannie Longo-Ciprelli"                                       7 Cycling     
#> 10 "Merlene Joyce Ottey-Page"                                     7 Athletics

Top scoring male athletes:

#> # A tibble: 10 × 3
#>    Name                        Olympic_Games Sport        
#>    <chr>                               <int> <chr>        
#>  1 Ian Millar                             10 Equestrianism
#>  2 Afanasijs Kuzmins                       9 Shooting     
#>  3 Hubert Raudaschl                        9 Sailing      
#>  4 Francisco Boza Dibos                    8 Shooting     
#>  5 Rajmond Debevec                         8 Shooting     
#>  6 Piero D'Inzeo                           8 Equestrianism
#>  7 Raimondo D'Inzeo                        8 Equestrianism
#>  8 Paul Bert Elvstrm                       8 Sailing      
#>  9 Durward Randolph Knowles                8 Sailing      
#> 10 Joo Filipe Gaspar Rodrigues             7 Sailing

To conclude this: The record is held by the Canadian Ian Millar, who appeared on 10 Olympic Summer Games over a time of 40 years!

Who won the most medals in any discipline?

From 1896 until 2016 a total of 39783 medals have been awarded. Of these 34088 were awarded at Summer Games, 5695 medals at Winter Games.

The different metals were distributed as such:

#> # A tibble: 6 × 3
#> # Groups:   Season [2]
#>   Season Medal      n
#>   <fct>  <fct>  <int>
#> 1 Summer Gold   11459
#> 2 Summer Silver 11220
#> 3 Summer Bronze 11409
#> 4 Winter Gold    1913
#> 5 Winter Silver  1896
#> 6 Winter Bronze  1886

The 30 top scoring female athletes, measured by total medals count⁷, are:

The 30 top scoring male athletes, measured by total medals count, are:

Top scoring male athlets, sorted descending by total medal count. To resolve ties, the medal_score values gold > silver > bronze (See. code for calculation).

Top Scoring NOCs

First let’s count the number of medals won by NOC:

Now, one might say, that there is at least one question arising: as you can see in Figure 2, some nations did not participate from the start, so the total medal count is unfair. Let’s see what happens, if we devide the medal count by the number of Games each NOC appeared on: there’s quite some movement at the top of the list now:

Another question is: “What if we normalized for the number of athletes that are being sent by the NOCs?” Read on to the next section to find out about this.

Note, that due to historic territorial changes, the Soviet Union (URS) and Russia (RUS) appear separately, as does the EUN, the “Unified Team at the Olympics” that only participated in 1992 as a temporary successor to the URS, until the former constituent states of the Soviet Union could register their own NOCs with the IOC. Similarly, East and West Germany (GDR and FRG respectively), appear separate from the now unified Federal Republic of Germany (GER). This might be the case for even more NOCs, however the above mentioned historically separate NOCs affect members of the Top 10, which is why I mentioned them.

TIL: at the 1952 Olympics in Helsinki, the Saarland sent their own athletes as separate NOC recognized by the IOC (no medals won that year). Four years later at Melbourne their team had already merged with the NOC of Western Germany. Before that however in 1954 the Saarland won the World Cup in Womens’ Canoeing.

Now let’s have a nice visualization of the top scoring NOCs (in absolute medal counts) to wrap up this section.

Bar chart race of the Top 10 NOCs for the total medal count over 120 years. NOCs: USA (United States of America), URS (Soviet Union), GER (Germany), GBR (Great Britain), FRA (France), ITA (Italy), SWE (Sweden), CAN (Canada), AUS (Australia), RUS (Russia), HUN (Hungary), FIN (Finland), NOR (Norway), BEL (Belgium), GDR (East Germany)

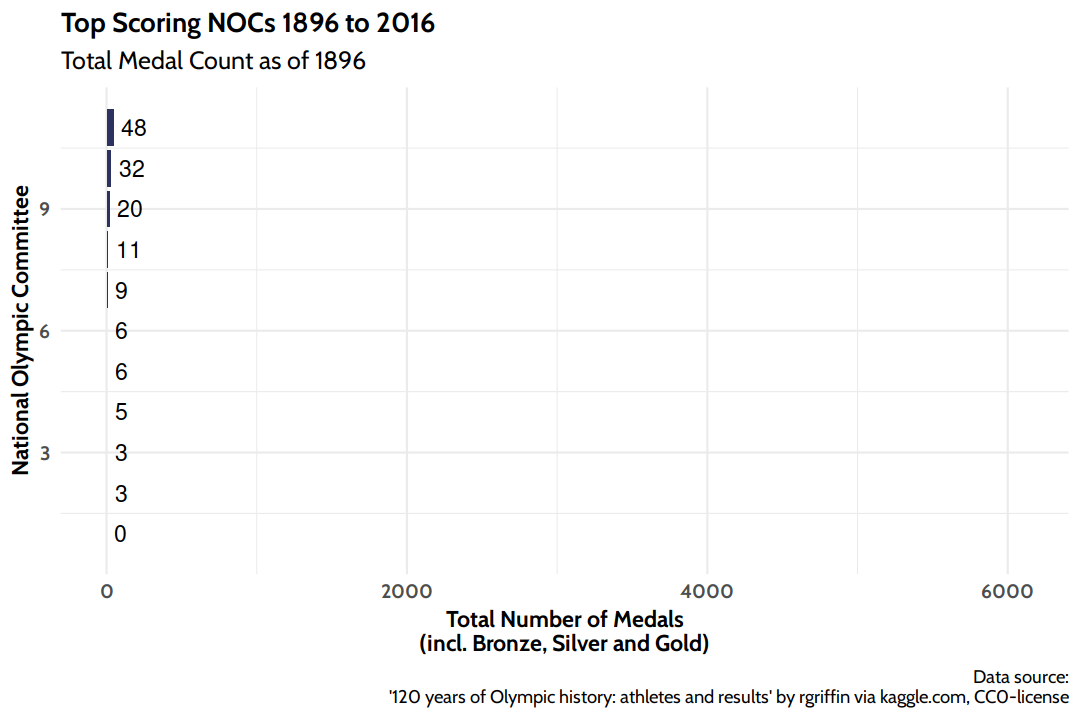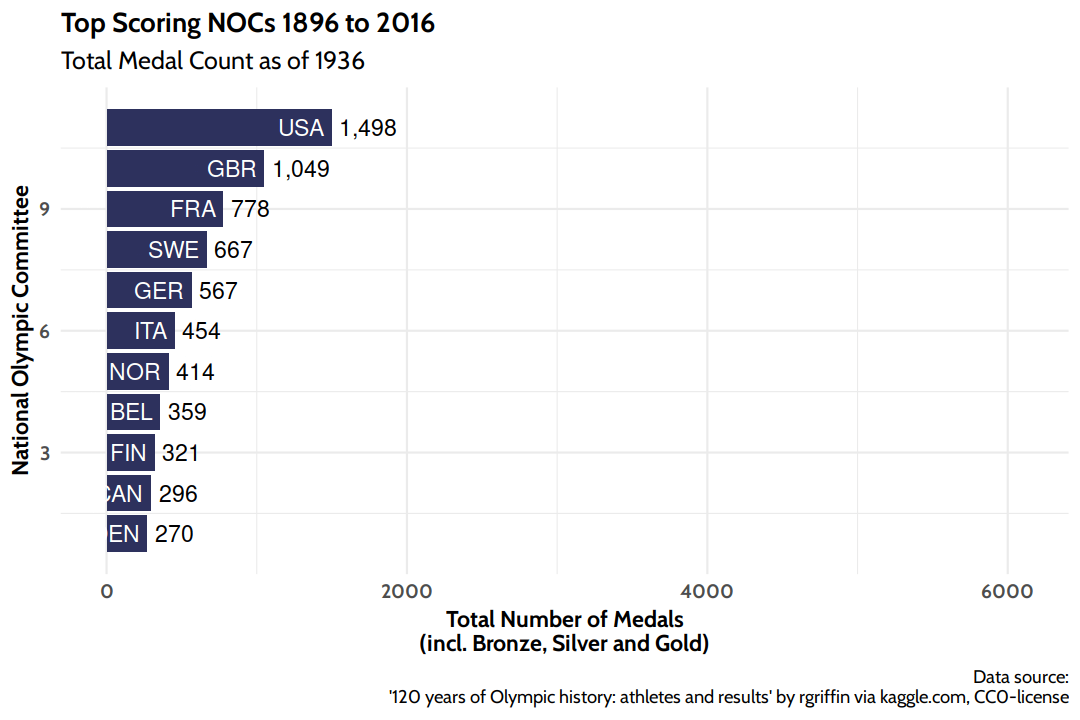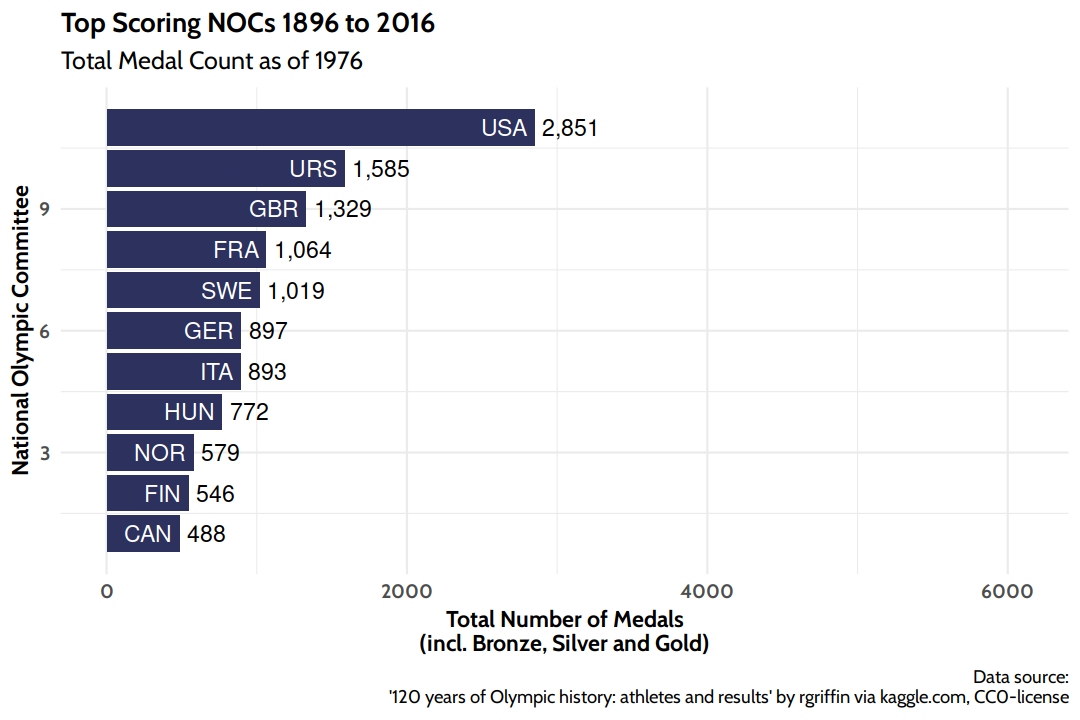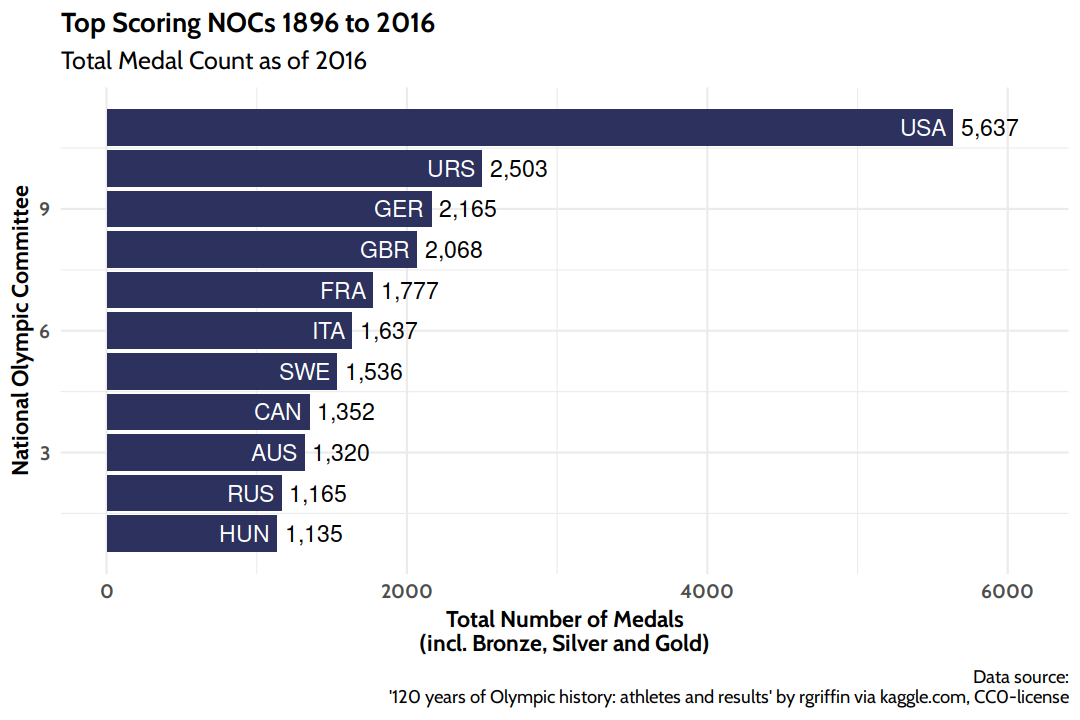
Does money buy medals?

Let’s hypothesize that two factors are important for the number of medals an NOC wins: number of athletes sent and the wealth of a country that influences the quality of training and also the number of trained athletes. So the first step is to analyze the relationship between GPD per capita and number of athletes. With this we can better intepret the influence of both on the Medal count.

Incorporating the Gapminder data

Preparation of the data

• the gapminder income dataset (GDP per capita) is read from file
• luckily the countrycode function can directly convert country names to IOC-Codes (i. e. NOC codes), so we can add those easily.
• in addition the gapminder population data is read
• both gapminder datasets are in wide format and have to be pivoted to a long form (pop_long and gapminder_long), I then filtered them to the years with Olympic Games⁸

“GDP per capita measures the value of everything produced in a country during a year, divided by the number of people. The unit is in international dollars, fixed 2011 prices. The data is adjusted for inflation and differences in the cost of living between countries, so-called PPP dollars.”⁹

Combining all the data

For this we need to…

• store the number of distinct athletes per Year and NOC in athlete_counts
• store the medal count per Year and NOC in gap_medal_count
• inner_join these two sets with gapminder_long and pop_long
• the ath_frac is calculated as the fraction of athletes sent by a NOC devided by the NOCs population in that year.

…so that in the end we have all data in long format in the gap_med_ath for analysis and plotting.

Correlation analysis

For an overview of the correlation between the population, GDP, athletes and medal count I chose a correlation matrix¹⁰ for the data in the year 2016:

Quick scatterplot matrix of the 2016 data in regard to possible correlations.

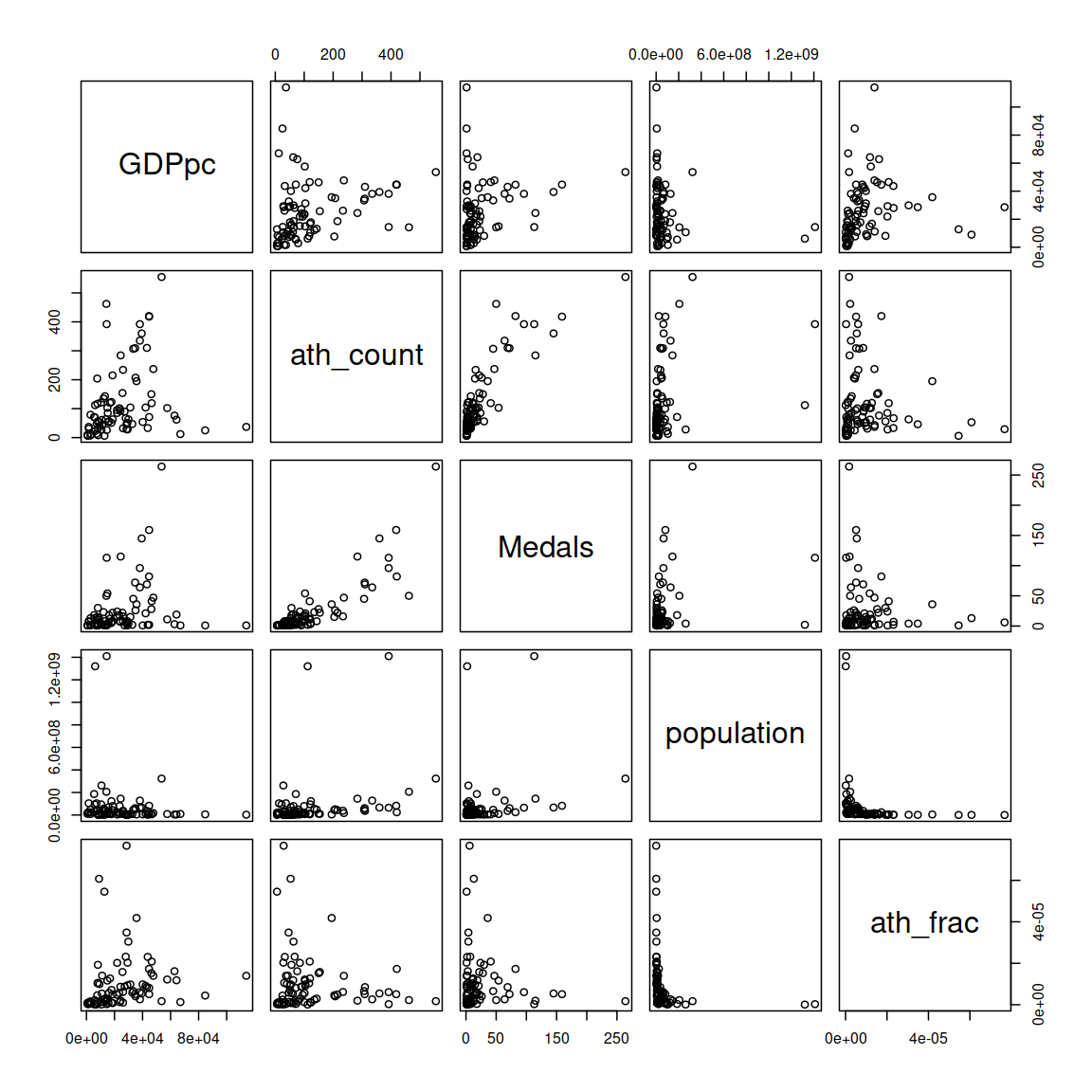
#>                 GDPpc ath_count    Medals population   ath_frac
#> GDPpc       1.0000000 0.3737319 0.2918326 -0.2419104  0.5041005
#> ath_count   0.3737319 1.0000000 0.8195948  0.4656754  0.1165829
#> Medals      0.2918326 0.8195948 1.0000000  0.3446223  0.1658349
#> population -0.2419104 0.4656754 0.3446223  1.0000000 -0.7816651
#> ath_frac    0.5041005 0.1165829 0.1658349 -0.7816651  1.0000000

There seems to be a moderate positive correlation between GDP per capita and athlete fraction (rho = 0.5041005). If we test this correlation we get a quite strong significe for this correlation as well:

#> 
#>  Spearman's rank correlation rho
#> 
#> data:  cor_dat$GDPpc and cor_dat$ath_frac
#> S = 45564, p-value = 1.377e-06
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#>       rho 
#> 0.5041005

Other correlations between GDP vs. absolute athlete count, as well as GDP vs. Medal count were - at best - weak, yet highly significant:

#> 
#>  Spearman's rank correlation rho
#> 
#> data:  cor_dat$GDPpc and cor_dat$ath_count
#> S = 57542, p-value = 0.0005431
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#>       rho 
#> 0.3737319

#> 
#>  Spearman's rank correlation rho
#> 
#> data:  cor_dat$GDPpc and cor_dat$Medals
#> S = 65067, p-value = 0.007808
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#>       rho 
#> 0.2918326

#> 
#>  Spearman's rank correlation rho
#> 
#> data:  cor_dat$ath_count and cor_dat$Medals
#> S = 16576, p-value < 2.2e-16
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#>       rho 
#> 0.8195948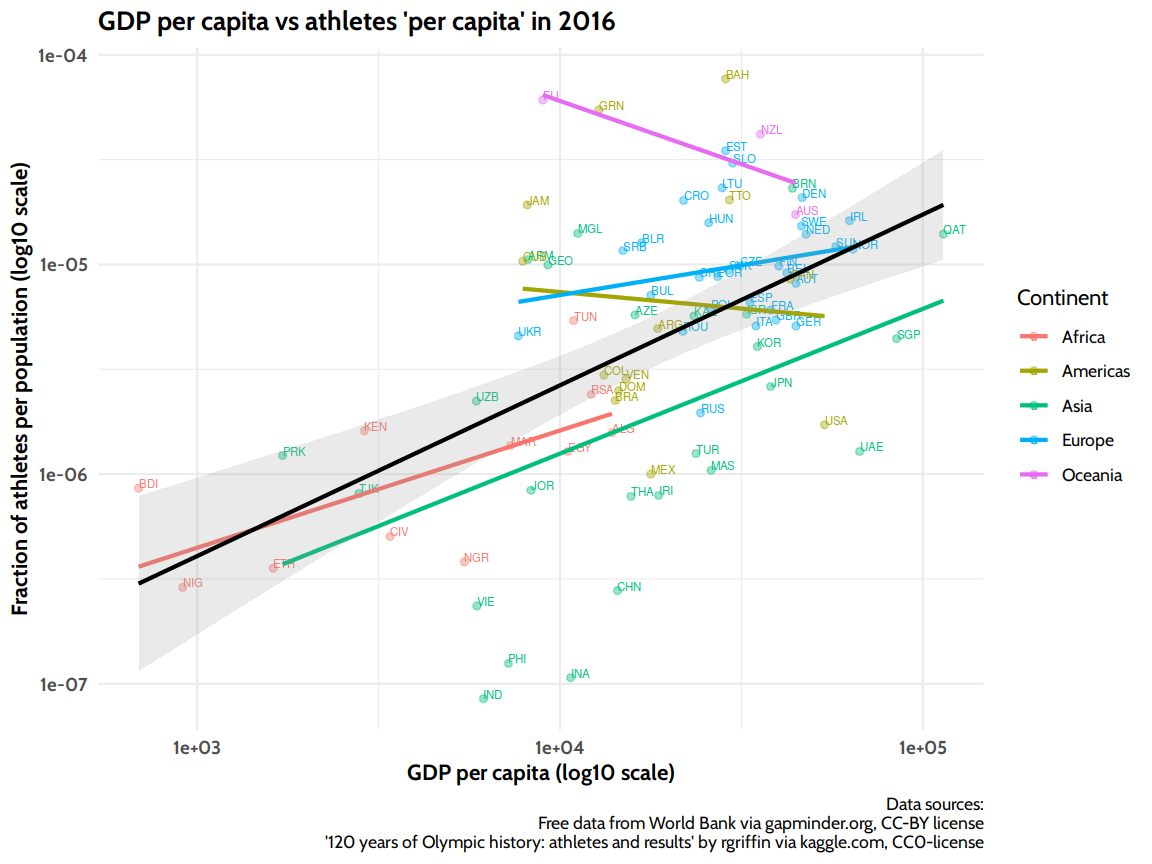

When looking at the plot above, we can see the overall positive correlation between GDP and athletes ‘per capita’ (black line), however the correlation depends on the continent! The positive trend is largest for African and Asian countries, moderate for Europe and even slightly negative for the Americas and Oceania. We could go deeper into that here, but that’s beyond the scope of this already long post. I’m happy if you read this far at all!

Bringing it all together

You might have noticed, that I didn’t mention the strongest correlation in the matrix above at all: Medals vs absolute athlete count correlated with a rho of 0.8195948! We probably wouldn’t need a significance test here¹¹, but while we’re at it:

#> 
#>  Spearman's rank correlation rho
#> 
#> data:  cor_dat$Medals and cor_dat$ath_count
#> S = 16576, p-value < 2.2e-16
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#>       rho 
#> 0.8195948

How could we bring all the interesting bits of information together here? By plotting the two factors GDP and athlete count on each axis and mapping the Medal count to the size of the “bubbles”:

#> 
#>  Spearman's rank correlation rho
#> 
#> data:  gap_med_ath_2016$ath_count and gap_med_ath_2016$Medals
#> S = 16576, p-value < 2.2e-16
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#>       rho 
#> 0.8195948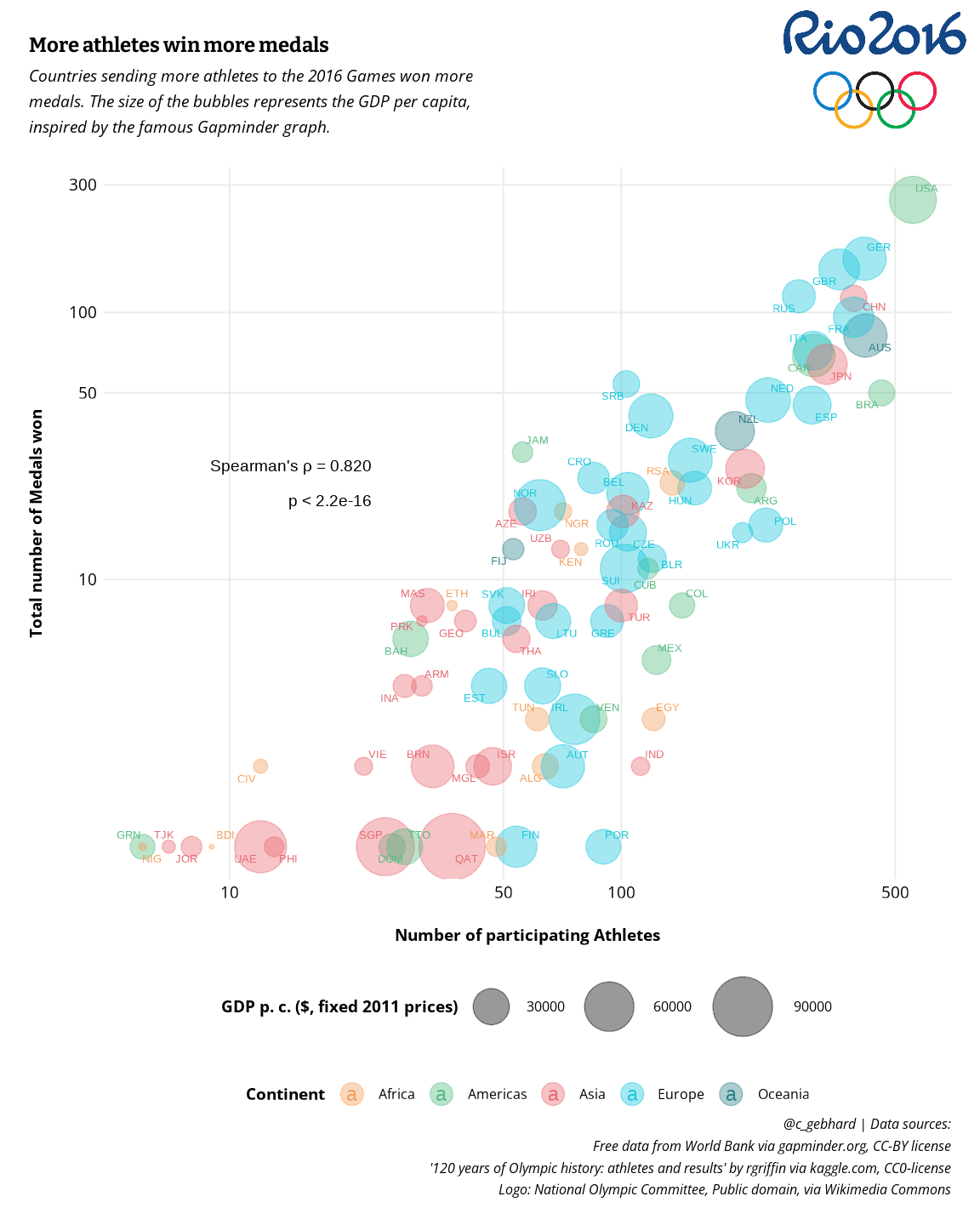

Medal Count in regard to GDP per capita and Athlete Count in 2016. I refreshed this graph for #TidyTuesday week 31/2021.

#>                                              statistic 
#>                                             "45563.74" 
#>                                              parameter 
#>                                                 "NULL" 
#>                                                p.value 
#>                                        "0.00000137709" 
#>                                               estimate 
#>                                            "0.5041005" 
#>                                             null.value 
#>                                                    "0" 
#>                                            alternative 
#>                                            "two.sided" 
#>                                                 method 
#>                      "Spearman's rank correlation rho" 
#>                                              data.name 
#> "gap_med_ath_2016$ath_frac and gap_med_ath_2016$GDPpc"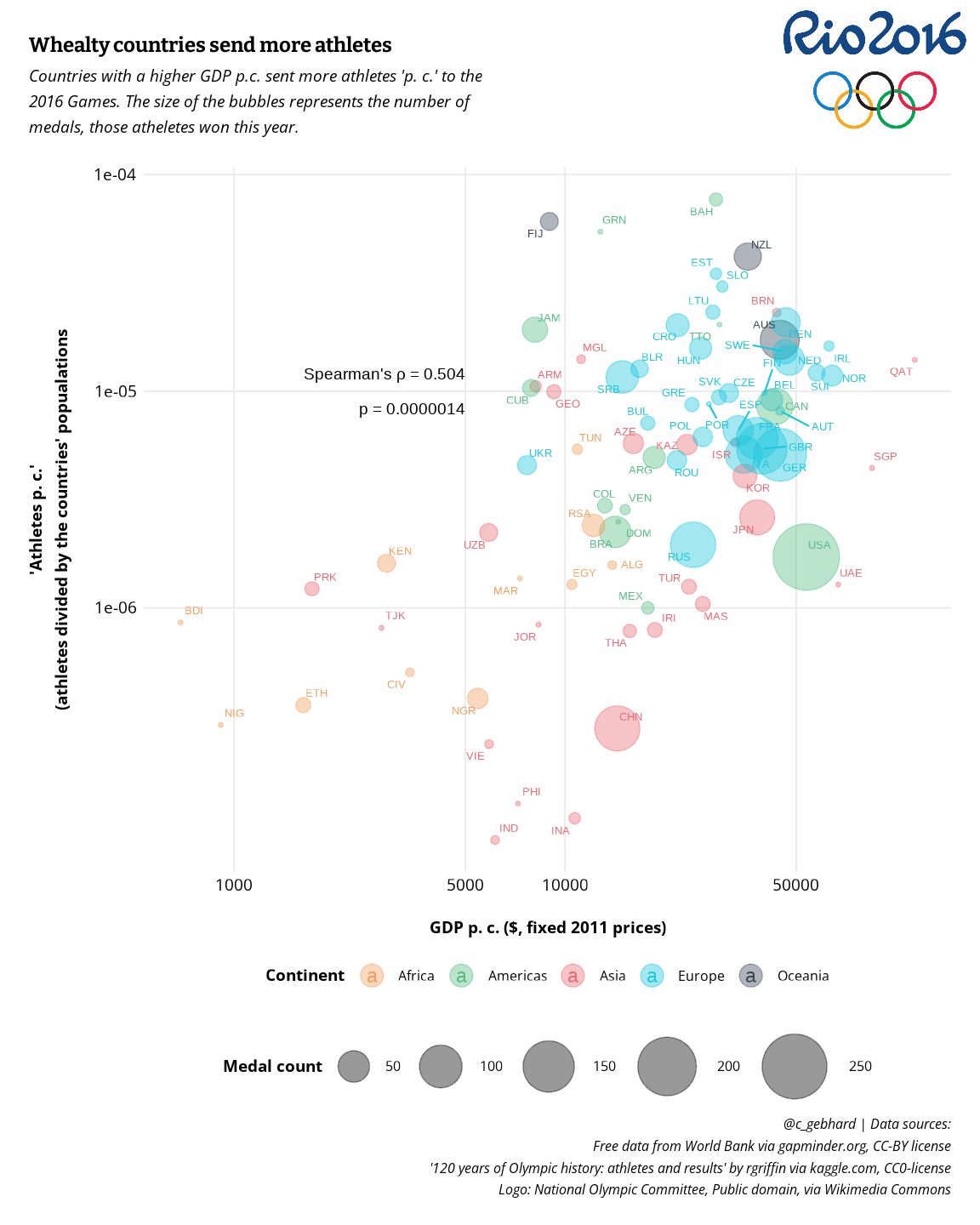

Athletes per capita vs GDP per capita: whealthy countries sent more athletes (in regard to their population) in 2016.I refreshed this graph for #TidyTuesday week 31/2021.

We see the strong correlation (rho = 0.8195948): A larger team sent to the Games returned a larger total number of medals.

Conclusions and Summary

• Most athletes participate only once at the Olympic Games, there are however a few exceptions of athletes who participated more often, even up to 10 times.
• In absolute numbers the USA and the former Soviet Union won the most medals (as of 2016). however if you put the medals into perspective of the number of participating athletes or the number of Olympic Games each NOC appeared at, there are some NOCs that were more successful at the few Games they participated at.
• There is a strong positive correlation between the number of athletes an NOC sends to the Games and the number of medals they bring home.
• There is a positive correlation between GDP per capita on the medal count. While statistically significant, this is a weak correlation and by all means you can’t infer any causation from this.

Footnotes

1. International Olympic Committee, https://www.olympic.org/

2. Or more correctly: is the number of medals won linked to the GDP per capita?

3. National Olympic Committees

4. https://www.gapminder.org/about

5. see https://www.olympic.org/international-judo-federation for more details.

6. notice the logarithmic scale on the y-Axis

7. To resolve ties, the medal_score values gold > silver > bronze (See. code for calculation)

8. this would be achieved by the later joining as well, but I felt it was better for the later performance on a machine with limited memory.

9. https://www.gapminder.org/data/documentation/gd001/, accessed 06.01.2021

10. I chose method = "spearman" since the medal count is not normally distributed and I couldn’t assume normality for the other variables either.

11. that’s the spirit

Reuse

Citation

BibTeX citation:

@online{gebhard2021,
  author = {Gebhard, Christian},
  title = {Olympic History},
  date = {2021-01-01},
  url = {https://christiangebhard.com/posts/2021-01-01-olympic-history/olympic-history.html},
  langid = {en}
}

For attribution, please cite this work as:

Gebhard, Christian. 2021. “Olympic History.” January 1, 2021. https://christiangebhard.com/posts/2021-01-01-olympic-history/olympic-history.html.